METODO DE TRANSPORTE NOROCCIDENTE Y COSTO MINIMO.

 METODO NOROESTE. 

El método de la esquina Noroeste es un algoritmo heurístico capaz de solucionar problemas de transporte o distribución, mediante la consecución de una solución básica inicial que satisfaga todas las restricciones existentes, sin que esto implique que se alcance el costo óptimo total. 

Paso 1

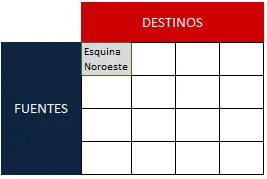
En la celda seleccionada como esquina Noroeste se debe asignar la máxima cantidad de unidades posibles, cantidad que se ve restringida ya sea por las restricciones de oferta o de demanda. En este mismo paso se procede a ajustar la oferta y demanda de la fila y columna afectada, restándole la cantidad asignada a la celda.

Paso 2

En este paso se procede a eliminar la fila o destino cuya oferta o demanda sea 0 después del «Paso 1», si dado el caso ambas son cero arbitrariamente se elige cual eliminar y la restante se deja con demanda u oferta cero (0) según sea el caso.

Paso 3

Una vez en este paso existen dos posibilidades, la primera que quede un solo renglón o columna, si este es el caso se ha llegado al final el método, «detenerse».

La segunda es que quede más de un renglón o columna, si este es el caso iniciar nuevamente el «Paso 1».

EJERCICIO METODO NOROESTE. 

METODO COSTO MINIMO. 

El método de costo mínimo es una técnica de análisis de decisiones que se utiliza en la toma de decisiones empresariales, especialmente en la gestión de la cadena de suministro y la logística, con el objetivo de seleccionar la opción más económica. Se trata de una herramienta que permite a las empresas optimizar sus recursos y maximizar sus beneficios al elegir el método de producción o logística más rentable.

¿Cómo se aplica el método de costo mínimo?

El método de costo mínimo se aplica a través de una serie de pasos que incluyen:

• Identificar los costos fijos y variables asociados a la producción del producto.
• Estimar la demanda del producto.
• Calcular el costo total de producción para diferentes niveles de producción.
• Calcular el ingreso total para cada nivel de producción.
• Calcular el beneficio para cada nivel de producción.
• Seleccionar el nivel de producción que maximiza el beneficio. 

EJERCICIO METODO COSTO MINIMO. 

MATERIAL DE APOYO DE CLASE. 

PROGRAMACION LINEAL.

Material de estudio. 

¿Qué es la programación lineal? 

Es una técnica matemática que se utiliza para optimizar el rendimiento o la eficiencia de un sistema. 

Pasos para resolver un problema mediante programación lineal. 

 1. Consiste en la identificación de los elementos básicos de un

modelo matemático, estos son:

◦ Función Objetivo

◦ Variables

◦ Restricciones

2. Consiste en la determinación de los mismos, para lo cual proponemos seguir la siguiente metodología:

Definir el criterio de la función objetiva. 

Identificar y definir la variable. 

Identificar y definir restricciones. 

planear la función objetivo. 

1) LA FUNCIÓN OBJETIVO

La función objetivo está directamente conectada con la pregunta principal que se quiere responder. Si un modelo tiene varias preguntas, la función objetivo se vincula con la de mayor importancia o la más fundamental. Por ejemplo, si el objetivo es minimizar costos, en realidad, la pregunta más relevante podría ser cómo aumentar la utilidad, en lugar de simplemente reducir gastos. 

2) LAS VARIABLES DE DECISIÓN. 

Las variables de decisión se relacionan con la función objetivo de manera similar a como los objetivos específicos se vinculan con el objetivo general. Estas variables se determinan a partir de preguntas que surgen de la pregunta principal del problema. En teoría, representan factores controlables dentro del sistema que se está modelando y pueden adoptar distintos valores. El propósito es identificar el valor óptimo de estas variables para alcanzar de la mejor manera el objetivo principal del problema. 

Ejemplo:

Imaginemos que una empresa de fabricación quiere maximizar sus ganancias (función objetivo). Para ello, debe tomar decisiones sobre cuántas unidades de dos productos diferentes debe producir (variables de decisión). Estas variables se identifican a partir de preguntas como:

• ¿Cuántas unidades del Producto A se deben fabricar?

• ¿Cuántas unidades del Producto B se deben fabricar?

Cada producto tiene costos de producción y genera ciertos ingresos, por lo que encontrar la cantidad óptima de producción permitirá maximizar las ganancias, que es el objetivo principal. 

3) LAS RESTRICCIONES – Limitantes (desigualdades – inecuaciones)

en un problema de programación lineal, las restricciones son los factores que limitan los valores que pueden tomar las variables de decisión. Para identificar estas restricciones, se recomienda imaginar un escenario en el que las variables puedan crecer sin límite (por ejemplo, producir infinitos zapatos en una fábrica). Esto ayuda a visualizar qué factores impedirían que esa situación fuera posible en la realidad.

Ejemplo:

Supongamos que una fábrica de pan quiere maximizar sus ganancias. Sus variables de decisión pueden ser:

• X: Cantidad de panes producidos al día.

Si intentáramos producir una cantidad infinita de pan, surgen varias restricciones como:

1. Materia prima limitada (harina, agua, levadura).

2. Capacidad del horno y equipo (no se pueden hornear panes sin límite).

3. Espacio de almacenamiento (el pan ocupa lugar).

4. Demanda del mercado (no hay clientes ilimitados para comprar pan).

5. Mano de obra disponible (número de trabajadores y horas de trabajo).

Estas restricciones evitan que las variables crezcan sin control y definen los límites dentro de los cuales se debe buscar la mejor solución. 

El método gráfico es una forma de resolver problemas de programación lineal, aunque solo se puede aplicar cuando hay pocas variables (dos en un gráfico 2D y tres en un gráfico 3D). A pesar de esta limitación, es útil porque permite interpretar los resultados y analizar cómo cambian ante diferentes condiciones. 

Este método funciona representando las restricciones como líneas o planos en un gráfico y determinando la región factible, que es el área donde se cumplen todas las restricciones. La solución óptima se encuentra en uno de los vértices de esta región debido a principios matemáticos relacionados con la geometría y la trigonometría. 

METODO SIMPLEX.

 .... 

METODO SIMPLEX.

VIDEO RESOLVIENDO UN EJERCICIO. 

¿Qué es el método simplex?

El método simplex es un algoritmo utilizado en la programación lineal para resolver problemas de optimización. En términos simples, busca encontrar la mejor solución posible a un problema dado, considerando ciertas restricciones y maximizando o minimizando una función objetivo.

Ventajas de utilizar el método simplex. 

• Aplicable a problemas de gran escala.

• Solución óptima.

• Flexibilidad en la formulación del problema. 

• Permite identificar soluciones no factibles o ilimitadas.

• Interpretación geométrica

• Puede incorporar variables no lineales

Problema:

$$Z = 3x_1 + 5x_2$$

$$2x_1 + 3x_2 \leq 8$$ $$4x_1 + x_2 \leq 6$$ $$x_1, x_2 \geq 0$$

---

Paso 1: Convertir a forma estándar

$$2x_1 + 3x_2 + s_1 = 8$$ $$4x_1 + x_2 + s_2 = 6$$

$$Z - 3x_1 - 5x_2 = 0$$

Variables no básicas: $x_1, x_2$.

Maximizar

Sujeto a las restricciones:

Las restricciones deben convertirse en ecuaciones agregando variables de holgura $s_1$ y $s_2$:

Función objetivo en forma estándar:

Variables básicas: $s_1, s_2$.

---

Paso 2: Tabla Inicial del Método Simplex

Básicas	$x_1$	$x_2$	$s_1$	$s_2$	RHS
$s_1$	2	3	1	0	8
$s_2$	4	1	0	1	6
Z	-3	-5	0	0	0